|
|
SYSTAT RESOURCES |
SigmaPLot : SIGMASCAN : TableCurve2D : TableCurve3D : PeakFIT : AutoSignal |
CONFIDENCE INTERVAL AND CONFIDENCE BANDS |
|---|
Basics
BASIC The UPPER and LOWER confidence limits for the estimated value of CANCER for each case will then be printed out. In the above, TIF stands for the "Inverse t-distribution." Using the Statistics->Regression->Linear dialog box or a command file, estimate your regression model again, remembering to save the results to a data file with MODEL option. The FREQUENCY command is very useful in this context; in calculating the regression, points with weight 1 will be used once, points with weight zero will be used zero times. Thus, the regression will be calculated for the cases with known values of Y and X. However, the value of ESTIMATE will be calculated for all cases. Using the file of saved results, you can use the calculation above to derive the confidence interval for the estimated mean of an unknown Y at a known value of X for the new cases. (In saving the results of the estimated model, SYSTAT renames the independent variables X(1). . . X(n), so that CARDIO is renamed X(1) in this example.) |
|||
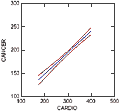
It is tempting to think that these lines form a confidence band for the entire line. That is not true. The problem is that the upper and lower confidence limits are calculated by using one point at a time. In order to calculate a confidence band or interval for an entire line, we need to take into account the fact that two parameters, the constant and the coefficient of X, are being calculated for that line. Therefore, upper and lower confidence bands for the entire line would be given by: LET n=48 LET nvars=2 LET upperband = estimate+SQRT(2*FIF(.95,2,n-nvars))*sepred LET lowerband = estimate+SQRT(2*FIF(.95,2,n-nvars))*sepred PRINT upperband lowerband RUN |
 |
||
When you plot the confidence intervals for the estimated values of CANCER and the confidence bands for the regression line, you'll see that the confidence band is wider than the confidence interval: |
|||
| BEGIN PLOT cancer*x(1) / SIZE=0 SMOOTH=LINEAR SHORT YMIN=100 YMAX=300 , XMIN=100 XMAX=500 XLABEL='CARDIO' COLOR=BLUE PLOT upper,lower*x(1) /SIZE=0 SMOOTH=SPLINE SHORT YMIN=100, YMAX=300 XMIN=100 XMAX=500 YLABEL=' ', XLABEL=' ' COLOR=RED OVERLAY PLOT upperband,lowerband*x(1) /SIZE=0 SMOOTH=SPLINE SHORT, YMIN=100 YMAX=300 XMIN=100 XMAX=500 YLABEL=' ', XLABEL=' ' COLOR=GREEN OVERLAY END |
|||
Because the relationship of CANCER (deaths per 100000 due to cancer) and CARDIO (deaths per 100000 due to cardiovascular disease) is linear, the difference between the confidence intervals for estimated values of CANCER and the confidence bands for the regression line is small, but even with well behaved data such as this the difference is apparent. LET n=48 LET nvars=2 LET s_square=177.065 LET upperband = estimate+TIF(.975,n-nvars)*SQR(sepred^2+s_square) LET lowerband = estimate-TIF(.975,n-nvars)*SQR(sepred^2+s_square) PRINT upperband lowerband RUN |
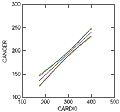 Click to view Larger Image |
||
where S_SQUARE is the mean square residual from the regression. These are sometimes called prediction intervals. When entering your values for N and NVARS, also enter the value for S_SQUARE, which you will find in the Analysis of Variance table of the regression output. |
|||
| BEGIN PLOT cancer*x(1) /SMOOTH=LINEAR SHORT YMIN=100 YMAX=300 XMIN=100, XMAX=500 XLABEL='CARDIO' COLOR=BLUE PLOT upperband,lowerband*x(1) / SIZE=0 SMOOTH=SPLINE SHORT, YMIN=100 YMAX=300 XMIN=100 XMAX=500 YLABEL=' ', XLABEL=' ' COLOR=GREEN OVERLAY END This will plot the confidence bands or prediction intervals around the data. |
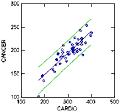 Click to view Larger Image |
||
|
|||