(7) New Curve Fitting Features

Curve Fitting Weight Variables may now be Specified Generally

Weight variables in the curve fitter may now be specified quite generally as functions of the parameters.  These weights will change at each iteration of the curve fitter which was not the case in previous versions.   As special cases this general specification includes the three new data weighting features:

• weighting by predicted values (a commonly requested and statistically desirable feature)
• weighting as a function of residuals (for robust regression)
• weighting as any function of the parameters (used by those that have measured their experiment errors in detail or know them from other's work)

Weighting by the predicted values is known to result in better curve fit statistics.  Robust regression will tend to ignore outlying data values and result in a better fit to the non-outlying data.  Some scientists perform replicate measurements to determine what the measurement error distribution is and then create a weighting function.  They can then incorporate these errors in the curve fit by using this predetermined weighting function.

Parameter covariance matrix and confidence intervals added to nonlinear regression reports

Two statistics have been added to the nonlinear regression report: 1) parameter confidence intervals and 2) the parameter covariance matrix.  Both can be used to obtain estimates of the error in the parameters of a curve fit.

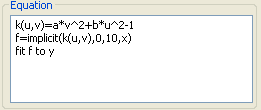
Implicit Function Curve Fitting

Implicit() can be very useful in curve fitting functions where the equation you want to fit is implicit.  An example of this occurs in drug synergy problems where the use of one drug causes the second drug to have a more potent effect.  The equations for a simple implicit function curve fit are shown below.

(8) New Statistics Features

(9) New Analysis and Transform Language Features

(10) New Graphing Features

(11) Application Support Features

(12) Macro Support Features

(1) Microsoft Office Style Ribbons

(2) New Property Browser

(3) User Interface Improvements

(4) Improved Graph Page Navigation

(5) Worksheet Improvements

(6) Report Improvements